曲線同士が接しているということは、その凸包も接していることになる。 凸包の共有部分を調べ、絞り込むことで交点を得ることが出来るだろう。 (凸包が全く同じ形状の場合、絞り込めないので、半分に切るなどの 対処が必要。)

なんとなく思いついた流れ

交点を求める( 曲線A, 曲線B){
　　　　if( ２つの凸包が接していない ) return null;
　　　　do{
　　　　　　　　clipA[] = 曲線A が、曲線Bの凸包内部である部分
　　　　　　　　clipB[] = 曲線B が、曲線Aの凸包内部である部分
　　　　}while( ClipA.length == 1 && ClipB.length == 1 && 収束していない );
　　　　if( ClipA.length ==  0 || ClipB.length == 0 ) return null;
　　　　if( ClipA.length == 1 && ClipB.length == 1 && 収束した ) return 座標;
　　　　result[] = {};
　　　　for( ClipA.length 回 ){
　　　　　　　　for( ClipB.length 回 ){
　　　　　　　　　　　　result +=  交点を求める( ClipA[cnt1], ClipB[cnt2] );
　　　　}　　　}
　　　　return result;
}

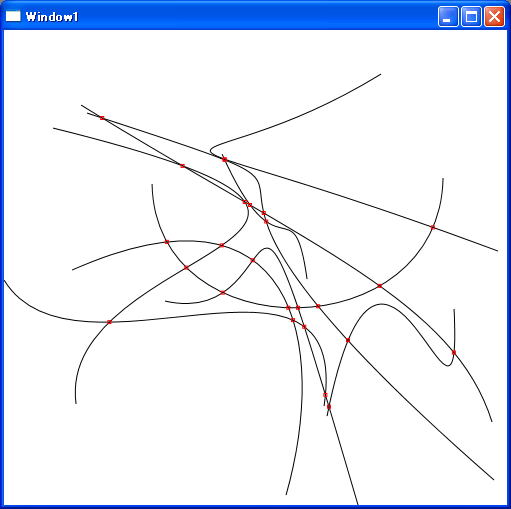
動作例

元の状態
２回処理後

最近作ったデモの画面

 

試行錯誤して気づいたこと

• 実数判定のため、虚数部の0チェックを厳しくしすぎるとうまくいかないことがあった。
• 収束判定がきつすぎて、凸包が細かくなりすぎて解を取りこぼした。
• 曲線が凸包内である区間を調べるときは、いったん t < 0, 1 < t の領域も含めた解をを得てから、マイナスだけの区間と1より大きい領域だけにある区間を省く。残った凸包内である区間の先頭がマイナスだったり、区間の終端が1より大きかった場合、それぞれ始点を0, 終点を1 とする。
• 同じ交点に収束する曲線同士だけを比較し、関係ない曲線から切り出されたものとは比較しない。