凸包とは、 Google検索：凸包

板の上に幾つも釘を打ち、外周から輪ゴムをかけて、 ゴムと接している釘で構成される多角形。

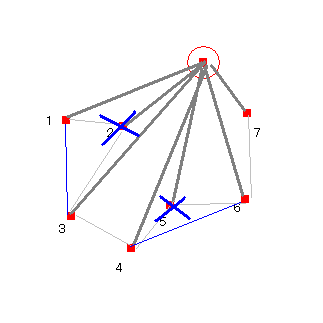
グラハムスキャン

まず、端にある点を基準として、それに対する角度の順に点を並び替える。

 

並び替えた順に点を見ていき、 一つ前の点H  現在の点I  次点J の角度∠HIJ が マイナスの場合、凹みであると判断して、点Ｉを削除する。

そして、その次の点Kとの ∠HJK を見る。

//凸包を得る
 static public Vec2D[] convex_hull(Vec2D[] points)
 {
	 List<KeyValuePair<double, Vec2D>> dict = new List<KeyValuePair<double, Vec2D>>();

	 //Y最小値を見つける
	 int max = 0;
	 for (int i = 1; i < points.Length; i++) {
		 if (points[max].y > points[i].y)
		 max = i;
		 else if (points[max].y == points[i].y && points[max].x < points[i].x) {
		 	max = i;
		}
 	}

	 //角度とともにlist に格納する
	 for (int i = 0; i < points.Length; i++) {
	 	if (i == max) {
			 dict.Add(new KeyValuePair<double, Vec2D>(0, points[i]));
		 } else {
			double theta = Math.Atan2(points[i].y - points[max].y, points[i].x - points[max].x);
			if (theta < 0) theta = 2 * Math.PI + theta;
			dict.Add(new KeyValuePair<double, Vec2D>(theta, points[i]));
 		}
 	}
	//ソートする
	System.Comparison<KeyValuePair<double, Vec2D>> cmp = new Comparison<KeyValuePair<double, Vec2D>>(cmpfunc);
	dict.Sort(cmp);

	//順に比較し、不要な点を排除していく
	List<int> del = new List<int>();
	for (int i = 1; i < dict.Count; i++) {
		int h = (i - 1 + dict.Count) % dict.Count;
		int j = (i + 1) % dict.Count;

		double theta1, theta2;
		theta1 = Math.Atan2(dict[i].Value.y - dict[h].Value.y, dict[i].Value.x - dict[h].Value.x);
		if (theta1 < 0) theta1 = 2 * Math.PI + theta1;
		theta2 = Math.Atan2(dict[j].Value.y - dict[i].Value.y, dict[j].Value.x - dict[i].Value.x);
		if (theta2 <= 0) theta2 = 2 * Math.PI + theta2;

	 	if (theta2 - theta1 < 0) {
			dict.RemoveAt(i);
			i--;
		}
 	}

	//戻り値用の配列に格納
	Vec2D[] result = new Vec2D[dict.Count];
	for (int i = 0; i < dict.Count; i++) {
		result[i] = dict[i].Value;
	}

	return result;
 }