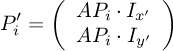ある直線 ax + by + c = 0; との交点が得られても、 その交点が2点の間にあるかを知るのは面倒なのではないかと思った。
考えてみて、このような方法を思いついた。
点A を原点とし、 点B に向かう直線を x軸としたローカル座標系を考える。
この座標系で、ベジエ曲線の y座標の式は、直線との距離を意味し、 x座標の式は、最も近い直線上の位置を意味する。
yの式が 0 で、 x の式が 0以上 、 AB の長さ以下なら、 交点が直線の上にあることになる。
まず、ローカル座標の x軸方向・y軸方向の単位ベクトルを作る
次に、ベジエ曲線の点を、ローカル座標に直す
小さい点は内積の意味。 2つのベクトルの x1 * x2 + y1 * y2 を計算する。
変換したローカル座標を元に、ベジエ曲線の式を作り、解く。->3次方程式を解く
これで、2点を結ぶ直線上に交点があることや、 直線上のどこに交点があるかを知ることが出来そう。
あと、ベジェ曲線の次数を減らせば線分同士の交点も求められる。
[試しに書いてみたソース]
public float[] intersection_line(PointF pa, PointF pb)
{
Vec2D vpta = new Vec2D(pa);
Vec2D vptb = new Vec2D(pb);
Vec2D vAB = new Vec2D(pa, pb);
Vec2D Ix = vAB / vAB.length;
Vec2D Iy = new Vec2D(-Ix.y, Ix.x);
Vec2D[] p2 = new Vec2D[4];
for (int cnt = 0; cnt < 4; cnt++) {
Vec2D AP = new Vec2D(pa, pts[cnt]);
p2[cnt] = new Vec2D(
Vec2D.inproduct(AP, Ix),
Vec2D.inproduct(AP, Iy));
}
Complex[] res = MyMath.cubiceq(-p2[0].y + p2[1].y*3 - p2[2].y*3 + p2[3].y,
3 * p2[0].y - 2 * p2[1].y*3 + p2[2].y*3,
-3 * p2[0].y + p2[1].y*3, p2[0].y);
List res2 = new List();
foreach (Complex v in res) {
if (v.imag < 0.0000001) {
double xval = (-p2[0].x + p2[1].x * 3 - p2[2].x * 3 + p2[3].x) * Math.Pow(v.real, 3) + (3 * p2[0].x - 2 * p2[1].x * 3 + p2[2].x * 3) * Math.Pow(v.real, 2) + (-3 * p2[0].x + p2[1].x * 3) * v.real + p2[0].x; if (xval >= 0 && xval <= vAB.length && 0 <= v.real && v.real <= 1) //追記
res2.Add(v.real);
}
}
float[] result = new float[res2.Count];
for (int cnt = 0; cnt < res2.Count; cnt++) {
result[cnt] = (float)res2[cnt];
}
return result;
}
[Vec2D クラス] 適当に作ったベクトルクラス
struct Vec2D
{
public double x;
public double y;
public Vec2D(double x, double y) //constructor
{
this.x = x;
this.y = y;
}
public Vec2D(PointF pt) //constructor
{
this.x = pt.X;
this.y = pt.Y;
}
public Vec2D(PointF pa, PointF pb) {
this.x = pb.X - pa.X;
this.y = pb.Y - pa.Y;
}
//演算子
public static Vec2D operator +(Vec2D c1, Vec2D c2)
{
return new Vec2D(c1.x + c2.x, c1.y + c2.y);
}
public static Vec2D operator -(Vec2D c1, Vec2D c2)
{
return new Vec2D(c1.x - c2.x, c1.y - c2.y);
}
public static Vec2D operator -(Vec2D c1)
{
return new Vec2D(-c1.x, -c1.y);
}
public static Vec2D operator *(double c1, Vec2D c2)
{
return new Vec2D(c1 * c2.x, c1 * c2.y);
}
public static Vec2D operator /(Vec2D c1, double c2)
{
return new Vec2D(c1.x / c2, c1.y / c2);
}
public static double inproduct(Vec2D c1, Vec2D c2) {
return c1.x * c2.x + c1.y * c2.y;
}
public double length
{
get{
return Math.Sqrt( x * x + y * y );
}
}
}